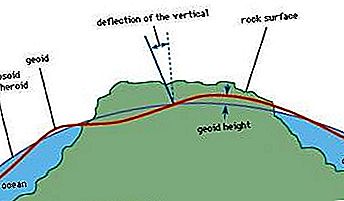
순열과 조합, 집합으로부터 객체가 대체없이 선택되어 서브 세트를 형성 할 수있는 다양한 방법. 이 선택 하위 집합을 선택 순서가 요인 인 경우 순열이라고하고 순서가 요인이 아닌 경우 조합을 말합니다. 17 세기에 많은 게임 기회에 대해 원하는 부분 집합의 수와 모든 가능한 부분 집합의 수의 비율을 고려하여 프랑스 수학자 Blaise Pascal과 Pierre de Fermat는 조합론과 확률론의 발전에 자극을 주었다.
조합론: 이항 계수
n 개의 객체는 한 번에 r 개의 n 개의 항목을 치환하는 것입니다. 순열 수는
순열과 조합의 개념과 차이점은 문자 A, B, C, D 및 E와 같이 5 개의 구별 가능한 객체에서 한 쌍의 객체를 선택할 수있는 모든 다른 방법을 검토하여 설명 할 수 있습니다. 선택한 문자와 선택 순서가 고려되면 다음 20 가지 결과가 가능합니다.

이 20 가지 가능한 선택을 각각 순열이라고합니다. 특히, 그것들은 한 번에 두 개씩 취해진 5 개의 객체의 순열이라고 불리며, 가능한 순열의 수는 5 P 2 기호로 표시됩니다. “5 permute 2”를 읽으십시오. 일반적으로, 선택할 수있는 n 개의 객체가 있고, 한 번에 k 개의 객체를 사용하여 순열 (P)이 형성되는 경우, 가능한 다른 순열의 수는 기호 n P k 로 표시된다. 평가 공식은 n P k = n! / (n − k)! 식 n! ("n factorial"로 표시)은 1에서 n까지의 모든 연속 양의 정수가 함께 곱해 짐을 나타냅니다. 그리고 0! 예를 들어,이 공식을 사용하면 한 번에 두 개씩 5 개의 객체를 치환하는 횟수는 다음과 같습니다.

(k = n의 경우, n P k = n! 따라서 5 개의 오브젝트의 경우 5! = 120 배열이 있습니다.)
조합의 경우 k 개의 객체가 n 개의 객체 세트에서 선택되어 순서없이 서브 세트가 생성됩니다. 이전 순열 예제와 해당 조합을 비교하면 AB 및 BA 하위 집합은 더 이상 고유 한 선택이 아닙니다. 이러한 경우를 제거함으로써 AB, AC, AD, AE, BC, BD, BE, CD, CE 및 DE의 10 가지 가능한 하위 집합 만 남아 있습니다.
이러한 부분 집합의 수는 n C k 로 표시되며 "n choose k"를 읽습니다. k 객체는 k! 준비, k가 있습니다! k 개의 객체를 선택할 때마다 구별 할 수없는 순열; 따라서 순열 공식을 k로 나눕니다! 다음 조합 식을 산출합니다.
이것은 (n, k) 이항 계수와 동일합니다 (이항 정리 참조). 예를 들어 한 번에 두 개씩 5 개의 개체를 조합 한 수는
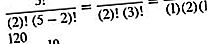
의 화학식 N의 P의 K 및 N C에서 k는 그들 모두 나열 할 필요없이 특정 상황 또는 치환 가능한 조합의 수를 계산하는데 사용될 수 있기 때문에 계산 수식 불린다.