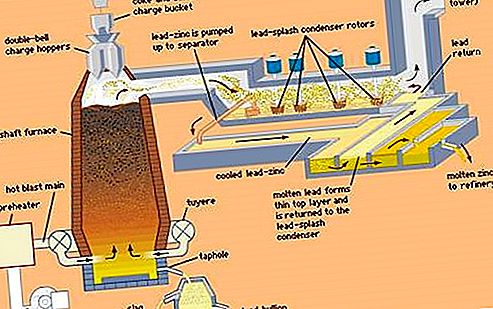
Chios의 히포크라테스 (fl. c. 460 bc)는 lunes로 알려진 원호 사이의 달 모양의 영역이 직선 영역 또는 직각으로 표현 될 수 있음을 보여 주었다. 다음의 간단한 경우에, 직각 삼각형의 측면 주위에 전개 된 2 개의 루네는 삼각형의 면적과 동일한 면적을가집니다.
-
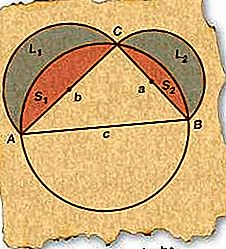
오른쪽 ΔABC부터 시작하여 지름이 빗변 인 AB (측 c)와 일치하는 원을 그립니다. 빗변을 위해 원의 지름으로 그려진 직각 삼각형은 원 안에 새겨 져야하므로 C는 원 안에 있어야합니다.
-
그림과 같이 직경 AC (b) 및 BC (a)로 반원을 그립니다.
-
그림에 표시된대로 결과 lunes L 1 및 L 2 및 결과 세그먼트 S 1 및 S 2에 레이블을 지정하십시오.
-
이제 루네의 합 (L 1 및 L 2)은 반원 (L 1 + S 1 및 L 2 + S 2)을 빼고 두 세그먼트 (S 1 및 S 2)를 뺀 것을 포함해야합니다. 따라서, L 1 + L 2 = π / 2 (b / 2) 2 -S 1 + π / 2 (a / 2) 2 -S 2 (원의 면적이 반지름의 제곱의 π 곱하기 때문에)
-
세그먼트 (S 1 및 S 2) 의 합은 AB에서 삼각형의 면적을 뺀 반원의 면적과 같습니다. 따라서, S 1 + S 2 = π / 2 (c / 2) 2 -ΔABC.
-
단계 5의 표현을 단계 4로 대체하고 공통항, L 1 + L 2 = π / 8 (a 2 + b 2 -c 2) + ΔABC를 제외합니다.
-
피타고라스 정리에 의해 ∠ACB = 90 °이므로 a 2 + b 2 -c 2 = 0입니다. 따라서, L 1 + L 2 = ΔABC.
히포크라테스는 반원보다 크거나 작은 원호에 여러 종류의 루네를 제곱 할 수 있었으며, 믿지는 않았지만 그의 방법이 전체 원을 제곱 할 수 있다고 암시했습니다. 고전 시대가 끝날 무렵, 유클리드 스 니펫의 라틴어 번역이 반 천년 동안 기하학의 빛을 깜빡이게하는 보티 우스 (c. ad 470-524)는 누군가가 원의 제곱을 달성했다고 언급했다. 공간이 부족하기 때문에 Boethius가 데모를 제공하지 않았기 때문에 미지의 천재가 루 네스를 사용했는지 아니면 다른 방법을 사용하는지 여부는 알려져 있지 않습니다. 따라서 그는 원의 구적의 도전과 함께 그것을 수행하는 데 분명히 유용한 기하학의 파편을 전달했습니다. 유럽인들은 계몽주의에 대한 불운 한 일을 잘 지켰습니다. 마지막으로 1775 년에 파리 과학 아카데미는 제출 된 많은 솔루션에서 오류를 발견하는 과제를 겪으며 서클 제곱과 더 이상 관련이없는 것을 거부했습니다.